"Vertical trails" approach
In this section we describe an experimental approach to indirect prediction of meteor activity which is base on the analysis of dust trails configuration when their direct encoonter with the Earth are absent. When we compute orbits of meteor particles, we factually trace the oribital evolution of trail central axis, or, in other words, of particles, ejected in tangential direction on the parent comet's trajectory at the moment of its perihelion. When the Earth encounters with such trails we call it "direct encounter". Also, earlier we presented an approach to analysis of non-perihelion particles parameters, which consider chances of conditions of encouneters between the Earth and particles, ejected not exactly at the moment of parent comet perihelion. In this section we'll also make a step aside, but this time not in temporal measurement, but in spatial one. We'll try to understand what to expect from "trail body", i.e. from particles, not belonging the central line of the trail, but lying slightly aside of it.
It's clear that in the reality trails are not very thin lines in space, but have quite substantial wide - tens or hundreds of thousands kilometers (depending on their age and perturbancies). This is the reason of quite lengthy meteor action when the Earth encounters dust trails and even when it doesn't pass very close to the axis of trail.
Someone could think that these thing are obvious and models many models, developed for meteor activity predition, are successfully used for already long time, and these models consider among other things the distance between the Earth and trail central line. Lets look at the Fig. 1 first:
It's clear that in the reality trails are not very thin lines in space, but have quite substantial wide - tens or hundreds of thousands kilometers (depending on their age and perturbancies). This is the reason of quite lengthy meteor action when the Earth encounters dust trails and even when it doesn't pass very close to the axis of trail.
Someone could think that these thing are obvious and models many models, developed for meteor activity predition, are successfully used for already long time, and these models consider among other things the distance between the Earth and trail central line. Lets look at the Fig. 1 first:
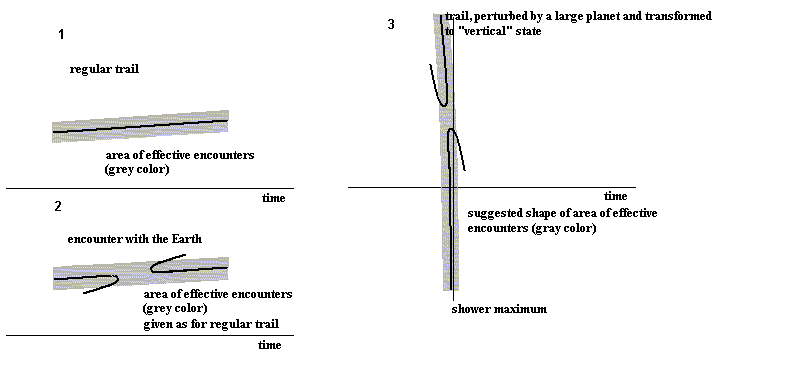
Fig. 1. Trail verticalization.
Situation 1. A regular trail with area of effective encounters aroud it (earlier we called it "trail body", it is depicted with grey color). If the Earth passes through this area, we have an encounter close enough for meteor outburst.
Situation 2. The same trail after encounter with the Earth. We can see typical lapels, consisting of perturbed particles, and a cavity between them. To be simple, we showed area of effctive encounter in its non-perturbed condition in order not to spend time for depiction of unnecessary curves.
Situation 3. The main one. We can see a trail after one or several encounters with strong sourses of perturbation (Jupiter, for example) which transformed it into "vertical" condition. In the reality it is not vertical, of course, but it looks so on the Fig. 1 - the particles with very different ejection velocities pass their minimal distances to the Earth's orbit at nearly one time (within a short period of time, at least). Compare to a regular trail - in this case times are different, but minimal distanse is nearly the same for all the trail. Such a "verticalization" is very frequient event in the streams of Jupiter family comets, perhaps it is also valid for Saturn family (such streams haven't been computed by us yet). The Leonids (Uranus family) also show this effect, but in lesser extent. For Perseids we haven't found signs of it. Perhaps it is connected with resonant movement, but we won't focus on this aspect now. The main idea is the following: particles in the area of effective encounters (trail body) should also be "verticalized". And it seems to happen. To demonstrate it we just showed the trail, suffed a local perturbation from encounter with the Earth. Resulting lapels are just in the area of effective encounters and can serve as "markers" of what happens to this area when central line of a trail gets verticalized. Orbital computations show that these lapels behave themselves as organic parts of the trail, i.e. they are also became verticalized (such verticalized lapels are shown on Situation 3). It is logical to assume, that area of effective encounters will also transform to a form, similar to one shown on the Situaltion 3 (it is also given as not perturbed by encounter with the Earth there). This leads us to an interestig conclusion: meteor activity can occur, if central line of vertical trail intersects the Earth's orbit close to the moment of shower maximum. In this case direct encounter can easily (enen most likely) will be absent - rD-rE value for direct encounter will have to high value, excluding the activity. This is also shown on the Situation 3.
The trail passes down, in the shown case it doesn't intersect at all the line of shower maximum, which reflects the moment of time, when the Earth passes stream nodes. Meanwhile, though the centrail line of the trail, as we can see, intersected the Earth's orbit shortly before the maximum, the Earth passes through the area of effective encounters. There is no close encounter with central trail line, because the latter during even 1-2 days (difference between the intersection of the Earth orbit and the Earth arrival to the point of intersection) will go very far to a vast distance for meteor outburst. But we still have such outburst. As an example we can take Draconids 1985. There was no direct encounter, but vertical 1946 trail intersected the Earth's orbit on 18 October, 10 days after Draconids maximum. We had a strong activity outburst. Basing on this case we eatimated, that 1 day of difference between the Earth's orbit intersection by the trail and the Earth's arrival to the point of intersection corresponds to nearly the distance rD-rE=0.00013 AU between the Earth on a regular trail (which is shown on the Situaltion 1). So far, and Draconids 1985 case 10 days difference means that the Earth passed, as it were, at the distanse 10*0.00013 AU = 0.0013 AU from trail particles, which intersected the Earth's orbit on 18 October.
We should give more detailed explanation of using a local perturbation for demonstration of "vertical trails" approach. It was depicted to show what happens to the trail body when its axis gets verticalized. After all we compute only these axis and they are the only things obviously knows. The trail body is like the "dark matter", which can't be detected but exists. In locally perturbed trail two lapels are formed, they consist of particles of trail axis - the "usual matter", shifted to the area of trail body ("dark matter"). Watching the behaviour of these lapels during trail verticalization we can understand the behaviour of "dark" trail body, because it is subject to the same forces as the lapels are. This is the reason to suppose that when trail axis gets verticalized, its body also verticalizes around the axis.
So far, along with analysis of non-perihelion particles we have two independent approaches to indirect forecasting of meteor activity, though they don't have a certain proofs of their validity. In other words, meteor showers can produce activity in three aspects - 1)during direct encounters with trails (traditional analysis); 2) when the Earth passes through areas on non-perihelion particles, in this case we have to calculate dT parameter, which is done for two neighbouring trails. This parameter characterises the place of cometary orbit where non-perihelion particles colliding with the Earth were ejected; 3) in case of "vertical trails" - when vertical trail intersects the Earth's orbit close to maximum time of the shower. Here we consider the single trail, i.e. results of the analysis doesn't depend on the place of neighbouring trails. Strictly speaking, direct encounter with a trail can be a particular case of 2 or 3 approach. For the second approach - when dT parameter is close to zero (but it is not true for all direct encounters). For the third approach - when vertical trail intersects the Earth orbit just in time when the Earth is in the intersection point.
2nd and 3d appoaches analyse particles, not belonging to the central trail axis, which consists of particles, ejected at the moment of parent comet perihelion in tangential direction to its velocity vector. But these approaches act in different dimentions. While 2nd approach considers particles, ejected not at the moment of parent comet perihelion, 3d approach analyses particles having radial components in ejection velocity, i.e. particles forming trail body around its central axis.
Usability of these approaches for each meteor activity case is different. Say, for Draconids 2005 only 2nd approach is applicable, for Draconids 1985 - 2nd and 3d approaches, for Draconids 2011 - traiditional analysis and 3d approach while in 2nd approach dT parameter values for different trail couple are close to 0.5, which exludes activity from non-perihelion particles.
Situation 2. The same trail after encounter with the Earth. We can see typical lapels, consisting of perturbed particles, and a cavity between them. To be simple, we showed area of effctive encounter in its non-perturbed condition in order not to spend time for depiction of unnecessary curves.
Situation 3. The main one. We can see a trail after one or several encounters with strong sourses of perturbation (Jupiter, for example) which transformed it into "vertical" condition. In the reality it is not vertical, of course, but it looks so on the Fig. 1 - the particles with very different ejection velocities pass their minimal distances to the Earth's orbit at nearly one time (within a short period of time, at least). Compare to a regular trail - in this case times are different, but minimal distanse is nearly the same for all the trail. Such a "verticalization" is very frequient event in the streams of Jupiter family comets, perhaps it is also valid for Saturn family (such streams haven't been computed by us yet). The Leonids (Uranus family) also show this effect, but in lesser extent. For Perseids we haven't found signs of it. Perhaps it is connected with resonant movement, but we won't focus on this aspect now. The main idea is the following: particles in the area of effective encounters (trail body) should also be "verticalized". And it seems to happen. To demonstrate it we just showed the trail, suffed a local perturbation from encounter with the Earth. Resulting lapels are just in the area of effective encounters and can serve as "markers" of what happens to this area when central line of a trail gets verticalized. Orbital computations show that these lapels behave themselves as organic parts of the trail, i.e. they are also became verticalized (such verticalized lapels are shown on Situation 3). It is logical to assume, that area of effective encounters will also transform to a form, similar to one shown on the Situaltion 3 (it is also given as not perturbed by encounter with the Earth there). This leads us to an interestig conclusion: meteor activity can occur, if central line of vertical trail intersects the Earth's orbit close to the moment of shower maximum. In this case direct encounter can easily (enen most likely) will be absent - rD-rE value for direct encounter will have to high value, excluding the activity. This is also shown on the Situation 3.
The trail passes down, in the shown case it doesn't intersect at all the line of shower maximum, which reflects the moment of time, when the Earth passes stream nodes. Meanwhile, though the centrail line of the trail, as we can see, intersected the Earth's orbit shortly before the maximum, the Earth passes through the area of effective encounters. There is no close encounter with central trail line, because the latter during even 1-2 days (difference between the intersection of the Earth orbit and the Earth arrival to the point of intersection) will go very far to a vast distance for meteor outburst. But we still have such outburst. As an example we can take Draconids 1985. There was no direct encounter, but vertical 1946 trail intersected the Earth's orbit on 18 October, 10 days after Draconids maximum. We had a strong activity outburst. Basing on this case we eatimated, that 1 day of difference between the Earth's orbit intersection by the trail and the Earth's arrival to the point of intersection corresponds to nearly the distance rD-rE=0.00013 AU between the Earth on a regular trail (which is shown on the Situaltion 1). So far, and Draconids 1985 case 10 days difference means that the Earth passed, as it were, at the distanse 10*0.00013 AU = 0.0013 AU from trail particles, which intersected the Earth's orbit on 18 October.
We should give more detailed explanation of using a local perturbation for demonstration of "vertical trails" approach. It was depicted to show what happens to the trail body when its axis gets verticalized. After all we compute only these axis and they are the only things obviously knows. The trail body is like the "dark matter", which can't be detected but exists. In locally perturbed trail two lapels are formed, they consist of particles of trail axis - the "usual matter", shifted to the area of trail body ("dark matter"). Watching the behaviour of these lapels during trail verticalization we can understand the behaviour of "dark" trail body, because it is subject to the same forces as the lapels are. This is the reason to suppose that when trail axis gets verticalized, its body also verticalizes around the axis.
So far, along with analysis of non-perihelion particles we have two independent approaches to indirect forecasting of meteor activity, though they don't have a certain proofs of their validity. In other words, meteor showers can produce activity in three aspects - 1)during direct encounters with trails (traditional analysis); 2) when the Earth passes through areas on non-perihelion particles, in this case we have to calculate dT parameter, which is done for two neighbouring trails. This parameter characterises the place of cometary orbit where non-perihelion particles colliding with the Earth were ejected; 3) in case of "vertical trails" - when vertical trail intersects the Earth's orbit close to maximum time of the shower. Here we consider the single trail, i.e. results of the analysis doesn't depend on the place of neighbouring trails. Strictly speaking, direct encounter with a trail can be a particular case of 2 or 3 approach. For the second approach - when dT parameter is close to zero (but it is not true for all direct encounters). For the third approach - when vertical trail intersects the Earth orbit just in time when the Earth is in the intersection point.
2nd and 3d appoaches analyse particles, not belonging to the central trail axis, which consists of particles, ejected at the moment of parent comet perihelion in tangential direction to its velocity vector. But these approaches act in different dimentions. While 2nd approach considers particles, ejected not at the moment of parent comet perihelion, 3d approach analyses particles having radial components in ejection velocity, i.e. particles forming trail body around its central axis.
Usability of these approaches for each meteor activity case is different. Say, for Draconids 2005 only 2nd approach is applicable, for Draconids 1985 - 2nd and 3d approaches, for Draconids 2011 - traiditional analysis and 3d approach while in 2nd approach dT parameter values for different trail couple are close to 0.5, which exludes activity from non-perihelion particles.